Carbon Sequestration: Is It Possible?
By Tom Murphy
30 September, 2011
Do The Math
You may have heard about the excess carbon dioxide in the atmosphere as a result of our combustion of fossil fuels. If we wanted to sweep the excess CO2 out of the air, what would it take? How much is there? Where would we put it? In this post, we will put the numbers in perspective and briefly examine a few of the possibilities for storage.
Setting the Scale
First, let’s explore a typical American’s annual contribution to CO2 to get some context. I will be drawing on methods developed in the previous posts on climate change and personal energy cubes, so if the numbers I pick seem to come from nowhere, check these pages for backup.
We know that the average American is responsible for 10 kW of continuous power production across all sectors of society, and that 85% of this is from fossil fuels. At a weighted average of 10 kcal/g of energy content in fossil fuels, and using the fact that every gram of fossil fuel combusted delivers 3 grams of CO2, we find that each kilocalorie of fossil fuel consumed produces about 0.3 g of CO2. At a rate of 8.5 kW of fossil fuel use, this turns into a whopping 175,000 kcal per day of consumption. Try to eat that much! So we end up with about 50 kg (110 lb) of CO2 per day per person.
Other useful calibrators: a tank of gas (10 gal, or ~40 L) produces 80 kg of CO2, and air travel produces 75 kg per passenger per 1000 km flown (and you thought your luggage was heavy!). Since I can’t resist comparing these numbers, a single-occupancy car beats air travel if it gets better than 66 MPG, and if two people are traveling, the car produces less CO2 once it gets better than about 33 MPG.
It’s a Gas
Let’s reflect on what we learned above: each American produces roughly their body weight in CO2 per day! At a density of about 2 kg/m³, this turns into 25 cubic meters, which would fill a bedroom with pure CO2 every day, per person.
Over a 40 year period, this accumulates to about 750 tons of CO2, occupying a cube 72 meters on a side. We can visualize these volumes relative to a house.
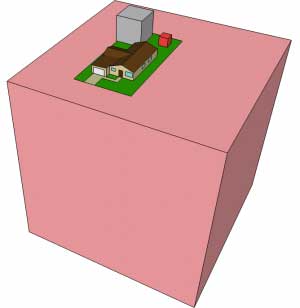
Volumes of CO2; in relation to a house. See text for details.
The red cube sitting in the back yard is the daily CO2 contribution per American. The much larger pink cube underneath the house represents a 40-year accumulation of one person’s CO2.
A Solid Result
Now we’ll abandon our gaseous state and look at a more practical packing for the purposes of sequestration: binding the CO2 into limestone, or calcium carbonate (CaCO3). I do not claim this to be an optimal solution, but CaO is the most abundant crustal oxide capable of forming a carbonate. Primarily, I pick on CaCO3 just to set a scale for visualization and to muse about where we’d put the stuff.
CaCO3 has a molecular weight of 100 g/mol and a density of 2700 kg/m³ (2.7 times water). Since CO2 has a molecular weight of 44 g/mol, every 44 kg of CO2 will end up producing 100 kg of CaCO3. Each person’s daily 50 kg CO2 contribution therefore produces a 115 kg cubic brick of limestone 0.35 m (just over a foot) on a side.
Over 40 years, we would produce a cube 8.6 meters on a side, seen as the gray cube in the back yard above. This house-sized behemoth is just for one person’s 40-year contribution. If we wanted to get back to the pre-industrial CO2 level of 280 ppm by volume (and equivalent restoration of ocean water), we would need to sequester 1200 Gton of CO2, so that each person on the planet would have a cube over 5 meters on a side.
Not in My Back Yard!
Where could we stash these giant bricks of limestone? They’re kind-of an eyesore in the back yard. In total, we’re talking about a Mount Everest-scale cube 10 km on a side. Wait a minute—didn’t we make a hole in the ground to extract the CaO in the first place? Yes, but this hole is only 45% the volume of the ultimate value-added brick. Maybe that’s half the battle, but half of a gigantic volume is still a gigantic volume. The point is not that we do not have enough room on the planet to accommodate these fantasy bricks of limestone, but just that they are not inconsequential things, at a personal scale.
I know! We’ll dump them in the ocean, and never speak of them again. Ironically, one of the disastrous consequences of CO2-induced climate change is sea level rise, yet if we drop our carbon bricks into the ocean, sea level will still rise! Are we hosed either way? Displacing a cube 10 km on a side in an ocean with a surface area of 0.72×4πR² = 3.7×1014 m³ would raise the level 2.7 mm. Whew. Were you scared?
Forest Green
Plants obviously offer a means to store CO2, if only temporarily. But planting a new forest and maintaining it in a mature state in perpetuity would represent a net decrease in atmospheric CO2. When I don’t know a subject very well, I try to come at it from as many angles as I can muster. If I get agreement, I feel I understand the problem. If I get disagreements within a factor of ten, I feel that I’ve got the basics right, but the mismatch is an indication of uncertainty. If I get wild disagreement, I figure I don’t understand the problem well enough to make confident and meaningful calculations. Let’s follow this approach for plants.
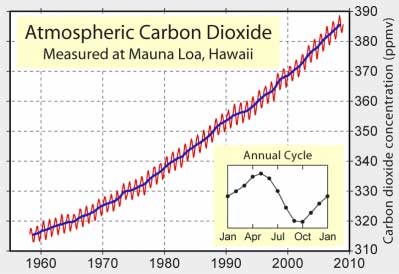
Atmospheric CO2 is rising around 1.9 ppm per year, also showing an annual cycle of 6 ppm peak-to-peak. Source: Wikimedia Commons.
What’s the scale? The first clue comes from the wiggles in the Keeling curve, showing an annual peak-to-peak variation of 6 ppm. This is the scale on which the global photosynthetic system (including plankton in oceans) currently manipulates CO2 levels. We need 18 times this to bring ourselves back to pre-industrial CO2 levels. Of course, the 6 ppm swing represents the seasonal “breathing” behavior of a roughly fixed stock of plants, and not the accumulated stock of locked-up carbon material. If one fourth of the photosynthetic activity leads to fixed mass (wood), and the average such tree/shrub lives 64 years, then we would see a fixed stock 16 times bigger than the annual sigh. These numbers are obviously contrived, but illustrate the point that the global photosynthetic system locks up about as much CO2 as the anthropogenic contribution. Therefore, to use plants as a means of getting back to pre-industrial levels, we would have to roughly double the current planetary scale of wooded land. This is far bigger than the typical green ad campaign of planting a few trees.
Another handle comes from the fact that the total global photosynthetic budget (oceans and land) is about 40 TW. The chemistry works out to about 3 grams of CO2 storage per kilocalorie of energy conversion. These numbers mean that 30,000 tons of CO2 are being “fixed” in plant matter every second. If the average growing season is six months, we lock up 400 Gt of CO2 each year. This is about one-third the amount of CO2 emitted so far by burning fossil fuels. In an equilibrium state, all of this returns to the air after the growing season, when the plants and leaves decay, and also when plants eventually die. The decay process gets stretched out over a period longer than six months, otherwise the CO2 annual cycle would show up as 30 ppm. I’m satisfied that these two handles from separate directions are self-consistent enough for me to proceed. But what about the fixed stock of wood? How much CO2 is stored in this form?
A mature forest might have a large tree every 5–10 m. Let’s split the difference and say that each tree occupies 50 square meters of land. We’ll make each tree trunk 0.5 m (20 inches) in diameter, and model it as a cylinder 30 m tall (about 100 ft). As an aside and a sanity check, we would expect our sight-lines in this forest to be 100 m before hitting a tree trunk (50 m² area density divided by 0.5 trunk diameter). Even though the trunk gets thinner and thinner as one climbs the tree, it has more and more branches. So I make things simple and use a straight cylinder. We end up with a stock of about 100 kg/m² of forestland, if wood is about the density of water. The dry weight—comparable to the CO2 uptake—is about half this, so we’ll say that each square meter of forest sequesters 50 kg of CO2. 28% of Earth’s surface is land, but most of this cannot support forest. Optimistically, let’s say one-third of the land area could carry a forest, or about 9% of the globe. I get a total forest mass of 2,400 Gt, or double our 1200 Gt contribution of CO2. The implication is that we would need 50% more forest on the planet to take care of the problem. I don’t know if the land could support this much more forest (how much deforestation has there been, globally?).
These methods are convergent enough for me to conclude that global-scale re-forestation can be part of a solution. It may not be feasible to rely on this alone, but it may well contribute enough to be meaningful.
Back in the Toothpaste Tube?
One appealing proposal for where to stash atmospheric CO2 is to inject it into spent oil and/or natural gas wells—perhaps even recovering reluctant oil by pressurizing the field. Could we use this tidy arrangement? Gas is far less dense than oil, but what about when pressurized for injection?
Each cubic meter of crude oil has a mass of about 850 kg, producing about three times this mass in CO2, or about 2500 kg. At atmospheric pressure, this occupies 1250 cubic meters—over 1000 times the underground volume we want to replace.
Typical oil wells are at a depth of one mile (1.6 km), where the rock overburden produces a well pressure of about 400 atmospheres (P = ρgh, where ρ ≈ 2500 kg/m³, g = 10 m/s², h = 1600 m, and Patm = 105 Pa). So our 1250 m³ gets compressed to 3 m³. One cubic meter of oil creates three cubic meters of appropriately-compressed CO2.
In other words, we could solve one third of our oil-generated CO2 problem by returning it to the well from which the oil derived. For natural gas, it’s a one-to-one ratio, since each CH4 molecule produces one molecule of CO2 upon combustion. And gases at a given pressure and temperature have the same number density.
It takes energy to compress the CO2 to 400 atmospheres, but only about 2% of the energy content of the corresponding oil.
I do not personally have the expertise to evaluate how leak-proof such a storage scheme would be. Geologically speaking, the caprock is able to hold natural gas and oil in place for millions of years. For reference, oil escaping at the rate of one drip per second would deplete a giant one-billion-barrel oil field in 75 million years. But does the story change after riddling the caprock with extraction wells whose caps/plugs may corrode or otherwise fail?
My sense is that it’s probably stable enough over relevant timescales, and could work to solve part of the problem for oil and gas. Doing the same replacement trick with coal is not possible. In fact, the mountain that used to sit atop the coal often no longer exists. But presumably other stable and impermeable geologic formations that played no role in fossil fuel extraction could also be used to hold CO2, so from this point of view, adequate storage may not be a real limitation.
Air Scrubber Scheme
But how might we recapture the genie from the air in the first place? A recent story on NPR described a prototype machine to suck carbon dioxide out of the air by passing air over plastic sheets dripping with sodium-hydroxide-laced water. The CO2 reacts with the sodium hydroxide to make sodium carbonate and water. The sodium carbonate solids are collected and sent to a natural gas burner, which liberates the CO2 for collection while the sodium ash is reunited with water to reform sodium hydroxide.
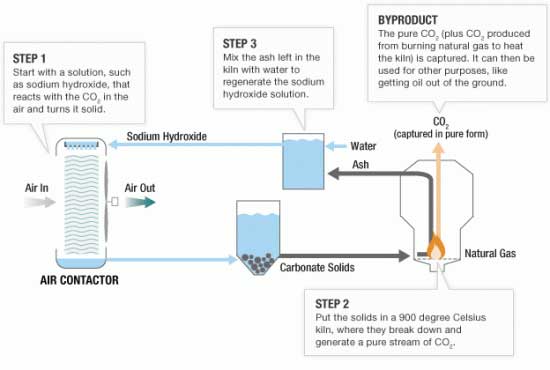
Source: Carbon Engineering; Credit: Nelson Hsu, NPR
Let’s evaluate this scheme in a model that we could scale as needed later. We’ll pull air in through a square opening one meter on a side. If we suck the air through the opening at 10 m/s (22 m.p.h.), we are dealing with 13 kg of air per second, and need to supply about 1500 W to the fan to give the requisite kinetic energy to the air at roughly 50% efficiency (windmills have a theoretical 59% maximum efficiency, for instance).
As a pure guess—likely overly optimistic—let’s say the device traps 50% of the CO2 gas entering the mouth. At 390 ppm by volume (590 ppm by mass) and 13 m³ per second, it captures 4 grams of CO2 per second. This makes 9 grams of Na2CO3, which must be heated to about 900°C to liberate its captured CO2. At a heat capacity of 200 J/kg/K, this requires a minimum energy of 1600 J. We need this amount of energy every second, or 1600 W of power. Our kiln will lose substantial heat to its local environment, so let’s say that the heating requires 3000 W of continuous energy input from natural gas (adding its own 0.15 g of CO2 per second).
If we add 500 W to run the other system components, we have 2000 W in (presumably) electricity and 3000 W in natural gas. The power plant consumes about 6000 W of primary energy to deliver 2000 W of electricity given the typical 35% efficiency, making our total primary energy input something like 9000 W—or roughly one standard American. We know from before that the 10 kW American profile results in 50 kg per day of CO2. If our 1 m² carbon capture device can pull 4 g per second out of the air, it will rack up 350 kg per day of CO2—while creating 50 kg in the process of generating the power (though presumably catching the 13 kg of CO2 that comes from its own natural gas).
I may be way off in my estimate of how much CO2 is removed from the air during its passage through the halls of sodium hydroxide. But the calculations indicate a significant margin over break-even operation, allowing for large leeway in the estimate. Unlike many news claims I evaluate, this one smells okay at first blush. I do not buy the statement that this technique could provide the CO2 used to push oil out of wells, thereby qualifying such oil as a low carbon fuel. We saw before that only a third of the oil-produced CO2 can replace the oil’s volume in the ground. So the oil effectively emits 2/3 as much carbon dioxide as it would otherwise. Maybe that qualifies it as “low carbon” by some standard. If so, it seems like a bad standard. In fact, to the extent that the oil is otherwise unrecoverable, the net effect is more CO2 in the atmosphere than would exist otherwise.
Finally, if we wanted to use such machines to stabilize CO2 at today’s level—assuming we could turn on enough units today—one-seventh of our total energy budget would be needed to run the units. If we wanted to drive ourselves back to pre-industrial levels we may need to double this figure. If my estimate that 50% of the CO2 can be scrubbed from the intake air is off, it could become as much as a factor of two easier in one direction, but who knows how bad in the other direction (imagine the right number is 10%, now five times harder , and risking less-than-break-even performance). This obviously isn’t the best way to offset all of our CO2 emission. Stationary emitters (power plants) are much better off collecting the CO2 at the source and not dispersing it far and wide for some hungry mouth to slurp up later.
Reality Check
Okay, after all this, I cheated and dug into the specs for the apparatus. There, I found an estimated energy requirement of 8.2 GJ to extract one ton (1000 kg) of CO2. My numbers above amount to a requirement of 9000 J to pull out 4 g of CO2, which turns into 2.25 GJ/ton. So I was indeed too optimistic by 3.6 times. Now the energy balance does not look as favorable, though it still exceeds the break-even threshold by about a factor of two. It should also be acknowledged that the fledgling machine may yet improve with time. So why do I leave the wrong calculations above? Because it illustrates the power in making estimates in Do the Math fashion. We had the basic idea right without a ton of work, complete with appropriate (original) caveats.
Some Perspective
As I have said before, I do not see climate change and CO2 as the largest immediate challenge we face when stood up against the crisis of finite fossil energy resources and a society built on the premise that they continue to be cheap and readily available. But it is certainly important and the two threats share a common solution in the aggressive reduction of our reliance on fossil energy sources.
Since we do not personally see the carbon dioxide flying out of our tailpipes and power plants, and the stuff has an entire atmosphere in which to disperse, we have little visceral appreciation for how much of this ethereal substance we are personally responsible for generating. Hopefully, the visualizations in this post help: it is far from an insignificant amount. Producing 50 kg per day of a gas is no small affair, and I could not even lift the daily brick I would generate out of CaCO3.
But more than the visualization exercises, we need to understand what is involved in capturing and sequestering CO2. I have often seen estimates that a coal-fired plant would spend 30% of its energy on capture and storage. My crude evaluation of the air-slurping idea was not too dissimilar for the “capture” part. At least the numbers come out on the positive side: we can get there from here—but at great expense. Thus far, I have seen no indication that we are willing to spring for a massive CO2 clean-up job, or to outfit power plants to eliminate their CO2 emissions. If fossil fuel shortages make everyone’s life harder and more expensive, we will have even less impetus to spend time, energy, and money on carbon clean-up.
Ironically, even though climate change and peak fossil production have a common solution in the deliberate reduction of fossil fuel use, they can also be inverse problems. That is, in the worst case of a crash caused by financial collapse in a post-peak declining world, the climate is spared (not necessarily fixed, just better than the IPCC scenarios). Conversely, if alternative fossil fuels (tar sands, heavy crude, oil shale, etc.) are up to the task of preventing a peak-induced crash, then the atmosphere had better watch out! In this case, we would find ourselves in the oft-quoted position that we’ll run out of atmosphere before we run out of fossil fuels. Of course, we could ignore both problems and they effectively go away, right?
Tom Murphy is an associate professor of physics at the University of California, San Diego. An amateur astronomer in high school, physics major at Georgia Tech, and PhD student in physics at Caltech, Murphy has spent decades reveling in the study of astrophysics. He currently leads a project to test General Relativity by bouncing laser pulses off of the reflectors left on the Moon by the Apollo astronauts, achieving one-millimeter range precision. Murphy’s keen interest in energy topics began with his teaching a course on energy and the environment for non-science majors at UCSD. Motivated by the unprecedented challenges we face, he has applied his instrumentation skills to exploring alternative energy and associated measurement schemes. Following his natural instincts to educate, Murphy is eager to get people thinking about the quantitatively convincing case that our pursuit of an ever-bigger scale of life faces gigantic challenges and carries significant risks.
Comments are not moderated. Please be responsible and civil in your postings and stay within the topic discussed in the article too. If you find inappropriate comments, just Flag (Report) them and they will move into moderation que.


